Potlucks and fractals

Last night, I was at a party thrown by a friend of mine.

This friend of mine lives at a house that has a potluck dinner most Wednesday evenings; I live three blocks away, so I go fairly often. I wasn't there last Wednesday, though, because it had been a long day and I was tired.

(Often there inadvertently seems to be a "theme" to the potluck despite nobody actually trying to do this, because pretty much any interesting-seeming coincidence counts. Last week it was the "night of the seven grains", as the seven people there brought dishes with seven different grains -- normal rice, arborio rice, buckwheat, wheat, two that I don't remember, and corn. Yeah, yeah, I know, you're thinking that arborio rice is rice. The point here is that if one interprets things widely enough there's always some sort of coincidence -- lots of today's foods are rectangular, or are yellow, or whatever. I think we once even said that the theme was "things with spices in them".)

While I wasn't there on Wednesday, people apparently came to discussing the existence of "some sort of crazy triangle fractal thing", and they had lamented that I wasn't there. I was eventually able to figure out that they were talking about the Sierpinski gasket, which is obtained by taking an equilateral triangle, removing a smaller triangle (half the size) from the middle to obtain three triangles with half the side length of the original triangle, and repeating ad infinitum. Click here for an illustration.

While this is nice, my favorite way to think of the Sierpinski gasket is via the so-called chaos game (more formally, an "iterated function system"), which is animated here. Start by picking three points (call them the red, yellow, and blue points) in the plane, and a random point x₀ in the triangle which they bound. Plot that random point. Now, pick one of the three corner points (red, yellow, or blue) at random, each with probability 1/3; then pick the point halfway between x₀ and that corner point, and call it x₁. Pick a corner point again at random; the point halfway between x₁ and that corner point is x₂. Do this a thousand times or so and you get a nice picture. An applet showing more examples of such iterated function systems is available at cut-the-knot.org.

Why does this work? Basically, if you take the whole Sierpinski gasket, and contract it by a factor of two towards one of its edges, you get one of its three self-similar parts; call these the "red", "yellow", and "blue" parts, as in the picture at left. 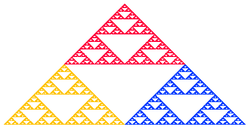Now, x₀ is some distance d from the gasket; the distance from x₁ to the gasket is d/2, the distance from x₂ to the gasket is d/4, and so on -- thus as the sequence is generated we get points closer and closer to the gasket. The gasket has measure zero, so with probability one we never actually end up with a point in it -- but we end up as close as we like after a very short time.

Although I'm not an expert in this, from some crude experimentation it looks like if you replace "each with probability 1/3" above with some other distribution, you end up with a gasket that is much more concentrated near the corners that you go to with high probabilities.

Edited, 5:06 pm: other surprising places where fractals appear include in the study of fast algorithms for multiplication (which also includes an explanation of the multiplication bug in Excel 2007), found via Good Math, Bad Math.